Voting Systems III – Representatives

This post is part of a series of posts on Voting Systems.

Now we move out of the simple realm of single offices and single issues. Appointing multiple politicians to represent a population is fundamental to the way in which most modern democracies work, but it is fraught with difficulty.

Proportional Representation (PR) refers to a government whose composition reflects the proportions of the population that support each party. The idea is that if 20% of the population support party A, roughly 20% of the government should be party A, etc.

That proportional representation is a desirable quality in a body of representatives shouldn’t be a controversial statement. Any particular demographic being underrepresented within the government will lead to a feeling of disenfranchisement and a loss of faith in the efficacy of a democracy. Alas, there are still a few arguments that are used to try to convince people that unrepresentative governments are somehow a good thing.

Representing Everyone

The main argument against PR seems to be that it results in coalitions rather than outright winners, and that coalitions are weak, ineffective and involve opaque “back-room deals”. This is something of a strange objection – firstly, there are many countries that do in fact use PR, and manage to get the job done just fine, so empirically they are not doomed to be ineffective. Secondly, back-room deals happen in every government – they are virtually the entire point of a politician’s job. It is hardly as though non-coalition governments can be relied upon to deliver every manifesto pledge without compromise. Aside from this, a good summary of the most common myths around PR can be found on the Electoral Reform Society website.

With the goal of proportional representation, you could divide the country up into small electoral districts that each elect a single politician, trying to keep the “single office” simplicity, but even using Approval Voting, the resulting set of representatives would be unlikely to be a fair representation of the population as a whole. Even in the absence of outright gerrymandering, these systems cannot reliably produce proportional representation, because parties with a moderate level of support that is spread out across a wide area will lose against parties whose support is more locally concentrated:

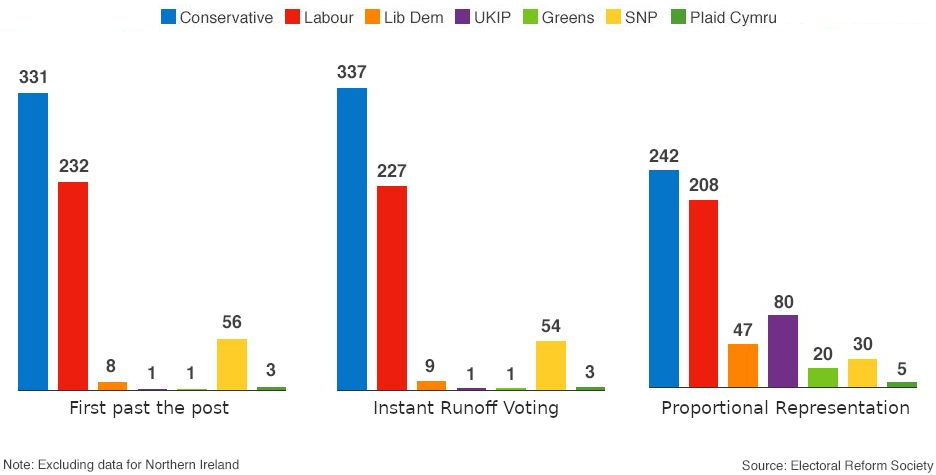
The 2015 UK General Election was one of the most disproportionate elections on record, but the issue has been know about for much longer than this and has been written about at length. As can be seen above, simulations suggest that IRV (2nd chart), with its single-seat districts does only a little better than the dreadful FPTP (1st chart), resulting in an array of representatives that are nowhere near the proportions that would accurately reflect the actual views of the population (3rd chart). Approval Voting with single-seat districts would be unlikely to fare much better, even if people felt more able to “vote with their hearts”, as each individual district would still be a “winner takes all” contest.

Instead, we can look at what is already in use. The main systems that are currently used to deliver a body of politicians that represents the populace proportionately are as follows:

• Mixed-Member Proportional (MMP) used in Germany as well as the Scottish Parliament, Senedd Cymru and London Assembly. CGP Grey has done a good explainer video on how this works.
• Single Transferable Vote (STV) used in Ireland, the Australian Senate and the Northern Irish Assembly. Another CGP Grey explainer video exists for this method.
• Party-list proportional using the D’Hondt method of apportionment, which favours larger parties and is used in Brazil and Austria.
• Party-list proportional using the Sainte-Laguë method of apportionment, which slightly favours smaller parties and is used in Norway and New Zealand.

Unfortunately, despite resolving many of the issues that are encountered when electing representatives, none of these are perfect. They are far superior to the methods used for the UK House of Commons and the US House of Representatives, but this is a very low bar indeed.

The STV method, which is a multi-seat version of IRV, is similarly non-monotonic, meaning that you can harm your candidate by voting for them. MMP and the party-list methods on the other hand place a heavy reliance on political parties themselves, allowing parties to punish politicians for disobedience by moving them down the party list, even if the public supports ideas that are outside of the party’s mainstream agenda. Ultimately, all of these are still voting methods that use ranked choices, meaning that they are “ordinal” methods to which Arrow’s Impossibility Theorem still applies.

Approvable Improvements

If we can’t get a proportional result by using Approval Voting to elect representatives to single-seat constituencies, is there a way to generalise Approval Voting to a multi-seat seat constituency that allows for some degree of proportionality?

The answer to this is yes – in fact there are several. Firstly there is Proportional Approval Voting (PAV), which uses a formula to calculate the “satisfaction” that voters gain from each possible set of winning candidates, and picks the candidates that maximise the population’s total satisfaction. This formula gives each person 1 unit of satisfaction for the first winning candidate that they approved, followed by a 1/2 unit for the second, a 1/3 unit for the third etc. Therefore, if there are 5 seats to fill and you approve of 4 of the 5 winning candidates, you are deemed to have a satisfaction of , while someone that approves of none of them would have a satisfaction of zero. This satisfaction function looks similar to the D’Hondt method of allocating winners in Party-list proportional representation, and in easy to analyse situations it delivers results that are proportional in the way you would expect. For example, in a 3 seat election with 2/3 of people in favour of party A’s candidates and 1/3 in favour of party B’s candidates, the result would be 2 candidates from A and 1 from B being elected.

Picking the candidates that maximise the population’s total satisfaction sounds like a good idea, but unfortunately it is enormously computationally complex. As the number of candidates grows, the number of calculations that must be performed grows super-exponentially, making it undesirable as a system to use on a large scale.

Thankfully, there are two relatively straightforward ways to simplify this system however. The formula to calculate the satisfaction can be simplified, yielding Satisfaction Approval Voting, or the search through the sets of winning candidates can be optimised using what is effectively a greedy algorithm, yielding Sequential Proportional Approval Voting.

Under Satisfaction Approval Voting, if a voter approves of n candidates, each of these approvals is counted as 1/n votes. Sadly, this would discourage people from voting for a large number of candidates, as their “satisfaction” with each candidate would be too small, making it likely that some of their vote would be wasted. This could reintroduce a kind of spoiler effect, in which a group of candidates that are similar to each other could either split the vote between them or cause people to spread their approval too thinly across the group, allowing less popular candidates with more concentrated support to win.

By using the original formula for satisfaction, Sequential Proportional Approval Voting (SPAV) avoids this issue – there is no disadvantage to voting for many candidates. Instead, the candidates are selected sequentially (rather than all at once, as under PAV):

1. The most approved of candidate is elected
2. All ballots that approved of that candidate are reduced in power to 1/2 of a vote
3. With these new weightings, the next most approved of candidate is elected
4. Ballots that approved of this new candidate are reduced in power – either from a full vote to 1/2 a vote, or if already at 1/2 a vote, they are reduced further to 1/3 of a vote
5. Continue in this manner until the required number of candidates have been elected

Although the sequential nature of the ballot counting might miss a slightly more optimal set of candidates that would be found under PAV, it makes for a much simpler process that is also faster to verify. As with any voting method, it is impossible to avoid all tactical voting, but SPAV eliminates most perverse incentives that other systems suffer from. A worked example of SPAV can be found at the Center for Election Science, and further discussion of its advantages can be found here.

I could stop here, with a recommendation that SPAV be used to elect any parliaments or representatives; replacing whichever methods are used currently. Indeed, this itself is probably a hard enough sell. I have however touched on another issue with democracies in a previous post: the pressure on politicians to pander to populism.

Sortition Revisited

The ease with which it is possible to sow division and discord for personal gain is one of the biggest problems that democracies are having to deal with in the current political climate. It is too easy to present a simple solution to a complex problem, and convince people to fall in line behind it. Through no fault of their own, a large number of people can ill afford the time and effort that would be required to inoculate themselves against such tactics.

This means that even with the perfect voting system, there are perverse incentives for politicians themselves. Rather than working together to solve problems, it is in their interest to perpetuate a problem but blame “the other side”. Intransigence becomes a virtue and compromise a weakness. The need to win re-election becomes more important to politicians than effective governance, so negotiation is replaced with grandstanding.

The United States Congress has terrible approval (worse than root canal surgery), and yet incumbents are usually re-elected. This is likely to be at least in part because of the incentive for the politicians to “throw the country under the bus” to benefit their particular constituents.

I mentioned a possible alternative approach previously, that I will quote here:

One potential solution to this balance is sortition – the way representatives used to be selected in ancient Athens.  This is a process similar to that used for jury duty, in which a number of members of the public who are citizens in good standing are selected at random to perform their civic duty.  Using sortition to select democratic representatives avoids the rat-race of election or re-election, reducing the pressure to pander to populism.  Its advantages are not simply limited to this however – the representatives being randomly selected from the population all but ensures that the majority of representatives are ordinary people, very much in touch with the wants and needs of the average citizen, rather than out of touch career politicians or technocrats.  Furthermore, given a large enough random selection, it can be made highly statistically likely that the selected people are a good representation of the population at large, which makes it likely that all interest groups are being represented.

It could be argued that since ordinary people do not tend to take the time to understand the nuances of policy normally, this would be a disaster.  However in the case of jury duty it is usual for people to take this civic duty very seriously, and when given leave from their job to perform this function, they have the time to look into any nuances in order to better understand them and make informed decisions.  In fact, there are studies suggesting that politicians that are more open minded and receptive to new perspectives may be less successful at being elected, which may mean that the amount of nuance that politicians are likely to be able to understand is less than that of the average person.

Using Sortition to generate a government body would ensure that it was representative of the population to a far greater extent than any system of voting could hope to do. It would also do away with the pressure of re-election, making the representatives free to compromise and find solutions that might be politically unpopular in the short-term.

This also completely removes the issue of voter apathy – the voters no longer have to vote, they simply have to be available to serve if called upon. In a similar manner to jury duty, the selected people would have to be given a sabbatical from their job, and remunerated appropriately, giving them time to familiarise themselves with the issues facing the government at the time. They would know that their voice mattered and that they only had a limited time to use it, which should incentivise them to understand the issues and do their best to reach decisions that benefitted the country and its people.

The suffrage by lot is natural to democracy; as that by choice is to aristocracy.  The suffrage by lot is a method of electing that offends no one, but animates each citizen with the pleasing hope of serving his country.

Montesquieu, The Spirit of Laws

Duration of Duty

At this point, there is an important implementation detail to consider – how long should these randomly selected representatives serve? Jury duty tends to last for a week or two, unless it is a particularly complex case, but this would be far too little time for a representative to be able to gain an understanding of the issues and have any hope of finding a resolution. On the other hand, members of the US House of Representatives have 2 year terms, so it can reasonably be considered that a representative has a chance to do something productive in 2 years, that can justify them running for re-election. 2 years is a long sabbatical for anyone to take however, so we should consider whether there is anything comparable that we can use to guide us.

Parental leave is a fairly widely applicable “sabbatical” that many people take at some point in their lives. In many countries, laws have been passed and great effort is made to stop companies from penalising or disadvantaging parents for taking parental leave. This is a desirable model, as we don’t want a system that disadvantages the randomly selected representatives. Chile, Venezuela, Poland, Czechia and New Zealand all offer around 6 months of maternity leave, and several other European countries offer significantly more, so this is a length of sabbatical that businesses have already adapted to work around. The UK is one of the most generous, offering up to a full year of maternity leave.

Based on this, it would seem that terms of between 6 months and 1 year would be manageable without significantly disadvantaging the representatives or the companies they work for.

This is significantly longer than Jury duty, but it would be quite reasonable to question whether this would still be too short of a time to do anything productive. It takes politicians a while to “learn the ropes”, becoming familiar with parliamentary procedure, and with all representatives being replaced every time, there would be a loss of institutional memory on a yearly or twice yearly basis.

I would argue that this is much less of an issue than it might initially appear. Firstly, much of parliamentary/congressional procedure is archaic and unnecessary – much of it revolves around political parties and manoeuvring which would not be relevant under sortition, with representatives that are not answerable to a party. Under the current system, the experience that politicians have in politicking is invaluable – knowing who to hobnob, and how to get leverage over a particular statesperson is essential for getting anything done, but this all becomes much less relevant when all of the other representatives are new as well.

Secondly, a lot of the machinery of government that must be navigated can be done with the assistance of civil servants. The UK government employs large numbers of steadfastly non-partisan permanent staff, who implement the policy of whichever government is in power. These civil servants provide an enormous institutional memory that transcends individual governments, so there is no reason to think that such a system would not cope with a more rapid turnover of representatives.

Thirdly, unlike in a technocracy, politicians in a democracy don’t need to be experts – they can requisition experts and advisors for whatever the issue is that they are dealing with. In fact, openness to the advice of experts is an important quality that many politicians unfortunately lack. The role of a politician is to interpret the advice and information they receive, think critically, and negotiate with the other politicians to take actions and pass laws that benefit their constituents and the country as a whole.

Democracy Without Voting

The question we are left with is: is sortition actually democratic? More specifically, can we guarantee fair representation under a system that uses randomness as its driver? This is where we start getting a little statistical, but it is worth it to iron out the wrinkles that are left.

For the sake of having nice round numbers to calculate with, let’s assume that we want to select 500 representatives (there are 435 seats in the US House of Representatives, and 650 seats in the UK House of Commons). Let’s also assume that our population is nice an evenly split in several different ways: 50% male and 50% female; 50% living in the North, 50% living in the South; 50% urban, 50% rural; 50% over-40, 50% under-40.

If we consider representation to be fair and proportional if it is within 3% of the actual split in the population at large, we would want no fewer than 47% female (or male) representatives, etc., which comes to 235/500.

If we do the simplest thing, and randomly select 500 representatives from the entire population, it initially looks like we are very likely to get a fair representation. There is only a 1 in 6 chance of randomly selecting 500 people from our population, and getting fewer than 235 males or females in our selection. It is possible to see this in Excel using the formula =2*BINOM.DIST(234,500,0.5,TRUE).

The trouble is, we mentioned four different ways that the population could be split 50/50, so we want to select a set of people that fairly represent all of these groups. If each of these splits is independant from one another (i.e. the North isn’t predominantly elderly, or the urban areas aren’t predominantly female, etc.), this makes it much less likely that we will achieve our goal. With four 50/50 splits, the probability of at least one of these groups having fewer than 235 representatives is slightly greater than 50%. The calcuation here is .

In fact, this gets even worse when the groups of people are smaller, as we end up with even more groups of people that need to be fairly represented. For example, in the UK, only about 2.9% of the population lives in Northern Ireland, so they should receive 14 or 15 of the 500 representatives. The probability of them receiving a number of representatives within the fairly wide range of 11 to 18 is actually only 72% =BINOM.DIST(18,500,2.9%,TRUE)-BINOM.DIST(10,500,2.9%,TRUE).

Thankfully, there is a very simple solution to this – we can keep the rough idea of constituencies and generalise it slightly. If we split the population into groups and select an appropriate number of people from each group at random, this ensures that each group gets the correct number of representatives. For example, a country could be split by age gender and location, giving the following 32 “constituencies”:

North, Male, 16-30	South, Male, 16-30	West, Male, 16-30	East, Male, 16-30
North, Male, 30-45	South, Male, 30-45	West, Male, 30-45	East, Male, 30-45
North, Male, 45-60	South, Male, 45-60	West, Male, 45-60	East, Male, 45-60
North, Male, 60+	South, Male, 60+	West, Male, 60+	East, Male, 60+
North, Female, 16-30	South, Female, 16-30	West, Female, 16-30	East, Female, 16-30
North, Female, 30-45	South, Female, 30-45	West, Female, 30-45	East, Female, 30-45
North, Female, 45-60	South, Female, 45-60	West, Female, 45-60	East, Female, 45-60
North, Female, 60+	South, Female, 60+	West, Female, 60+	East, Female, 60+

These constituencies don’t have to be exactly the same size, they just need to be large enough to warrant at least 1 representative. If we are representing a population of 50,000,000 with these 500 representatives, that means that each one represents 100,000 people, so a constituency of 400,000 people would need to have 4 representatives randomly selected from it.

Intersecting Identities

There is actually no reason why we cannot break the population down into other sensible groupings to ensure each gets proper representation. Different ethnicities within the population could be constituencies, ensuring that each is adequately represented, as well as different professions, different education backgrounds, parents, and LGBT people.

Clearly if all of these were combined with the 32 constituencies above, this would make an enormous number of individual groups, some of which would be far too small to warrant a representative. There is however a better way to manage this, that avoids this problem.

Let’s take medical doctors as an example: Italy and Spain have around 4 doctors per 1,000 people, so in a country with similar healthcare and a population of 50,000,000 we would expect 200,000 doctors. If we want representatives from all backgrounds and careers, in proportion to the population as a whole, we should be aiming to have 2 of our 500 representatives be medical doctors. We don’t really need to ensure that both doctors from the North and doctors from the South are represented, or that older doctors and younger doctors are represented. Both doctors being from the North is not an issue as long as the South has other representatives.

If we have the requirement, simply that North and South; old and young; doctors, teachers, farmers, etc. each have a proportionate number of representatives, it is possible to design a system that can reliably select these representatives.

In addition to the demographic groups given in the table above, this system allows us to specify as many other partitions of the population as we would like to represent, as long as every person is a member of a single category within each partition. This means that in the “profession” partition, you can’t be in both the “doctor” category and the “teacher” category. Also, it is necessary to have an “unemployed” category within this partition, so that every person gets a category.

A selection algorithm then proceeds as follows:

1. Start with the constituency/category with the smallest number of eligible people
2. Select a random member of this category
3. If this person being made a representative means that any of the categories of which they are a member are now fully represented, all people that are members of the fully represented category are removed from the pool of eligible people
4. Of the categories still needing representatives, take the category with the smallest number of eligible people and repeat until all representatives have been selected

Partitioned Sortition

This may all seem quite abstract, so I shall demonstrate with a worked example. This (somewhat simplified) civilisation consists of 500 people needing 10 representatives. There are:

• 252 men and 248 women
• 219 from the North and 281 from the South
• 45 government employees, 60 unemployed and 395 with private sector jobs
• Three different ethnicities – 49 Jovians, 103 Martians and 348 Terrans

This means that out of the 10 representatives, there need to be 2 men from the North, 3 men from the South, 2 women from the North and 3 women from the South. There also needs to be 1 government employee, 1 unemployed person and 8 privately employed people as well as 1 Jovian, 2 Martians and 7 Terrans.

In the image below, the particular category under sortition is highlighted red. Selected representatives gain a red ring, and people no longer in the eligible pool are greyed out. The partitioned sortition algorithm proceeds as follows:

Working through this step by step:

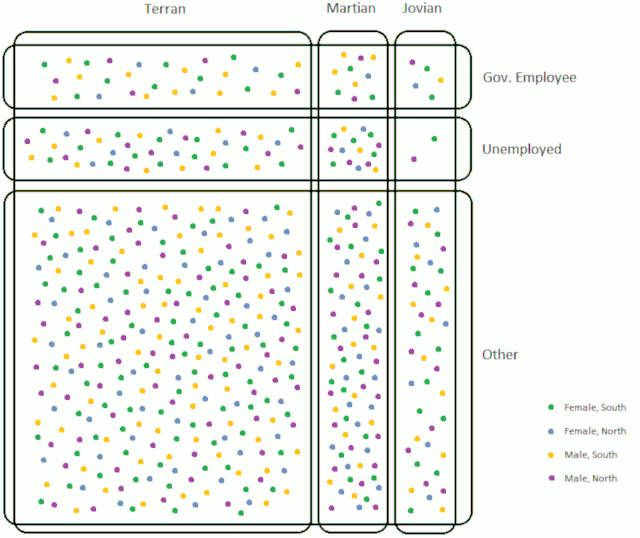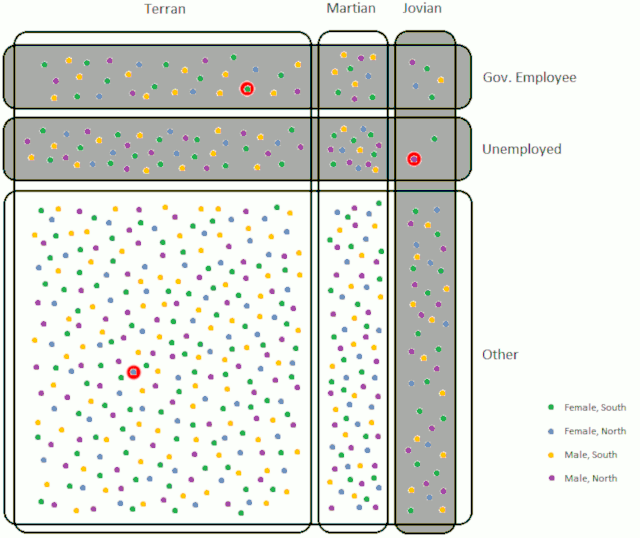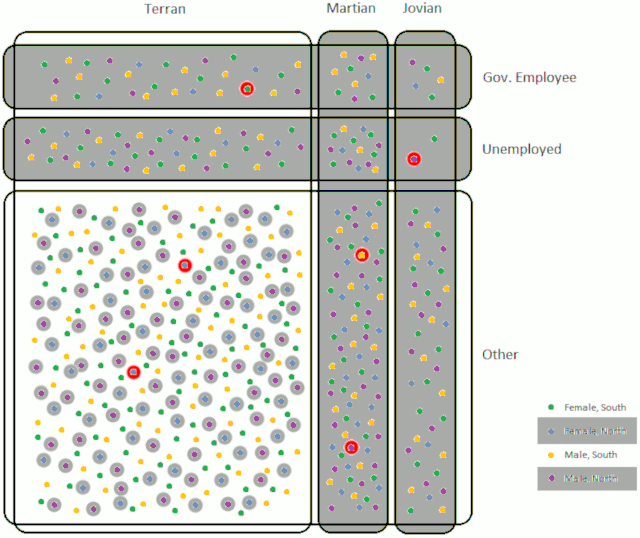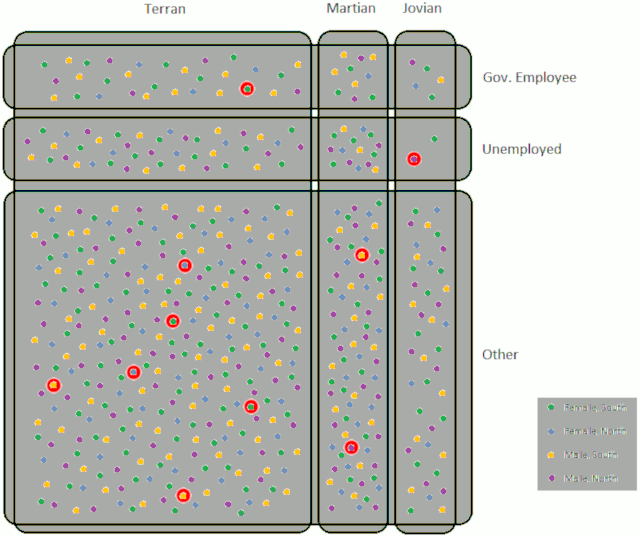
1. Initially, the smallest category is government employees with a population of 45. One is selected at random, and they are a Terran woman from the South. Government employees only need 1 representative, so this category is exhausted – we remove all remaining government employees from the elegible pool.
2. Having removed these people, the smallest category is Jovians with 44 members (5 of their initial 49 were government employees). One is selected at random, and they are an unemployed man from the North. Both Jovians and unemployed people only needed 1 representative, so both of these categories are exhausted.
3. The smallest category is now “Female, North” with 76 members (the blue dots). One is selected at random, and they happen to be Terran. No categories are exhausted.
4. As no other categories were exhausted, the smallest category remains the same, and another member is selected at random (they also happen to be Terran). “Female, North” only required 2 representatives, so this category is now exhausted and all people that are members of this category are removed from the eligible pool.
5. The smallest category is now Martian with 58 members. The selected representative is a man from the North. There are now 2 representatives for “Male, North” (the purple dots), so this category is exhausted, and its remaining members are removed from the eligible pool.
6. Martian is still the smallest category, so another Martian is selected – this time a man from the South. Martians only need 2 representatives, so this category is now exhausted.
7. The smallest category is now “Male, South” with 75 members (the yellow dots), so one is selected.
8. No categories were exhausted, so the smallest category remains the same and another member of “Male, South” is selected. This is the third representative of this category and only 3 are needed, so all remaining members are removed from the eligible pool.
9. There is only 1 remaining category within each partition of the population – Terran women from the South, in private employment. 2 people fitting these categories are selected at random.
10. We now have 10 random representatives that proportionaly reflect the gender, geographical, ethnic and employment splits of the civilisation.

Pathological Partitions

This is all very well, but is it possible to end up in some sort of bind where the random choices made earlier in the process make it impossible for you to select proportional representatives later?

The two smallest groups in the above example were government employees and Jovians. If instead there was a significant overlap between these two groups, with 40 people being both Jovian and government employees, we can see what would happen when picking the first representative (a government employee):

• If the government employee selected were a Jovian, this person serves as representative for both categories.
• If they were not Jovian, this selection would eliminate all remaining government employees, which would eliminate 40 out of the 49 Jovians. There would then only be 9 Jovians left, which would make them by far the smallest group, guaranteeing that a Jovian representative would be picked next.

Would it be possible to have a variant of this in which there are no Jovians left, leaving them unrepresented?

Well… No. If all Jovians were government employees, and a government employee were picked that was not Jovian that would be impossible. If there were a government employee that was not Jovian, this would mean that the number of government employees was larger that the number of Jovians, so the Jovian representative would get picked first. Alternatively, if all government employees are Jovians too, there is no-one that fits thes criterion of government employee but not Jovian.

This is not a mathematically rigorous proof that such situations are impossible, but it should serve as a sketch for how such issues are avoided by virtue of selecting from the smallest category first.

Verifiability

Another consideration is whether it matters if people’s membership in these categories is verifiable, or if people lying about their membership of a category is an issue. If a partition of the population is based around a quality that is hard to verify or based on self-identification, what happens when someone is miscategorised?

I will argue that it is in fact a very minor issue indeed, due to the inherent fairness built into the original concept of sortition before we introduced the partitioning.

Let’s take a “worst-case” scenario, in which someone is not just miscategorised, but is in fact malevolently claiming membership of a category in order to stand a chance of selection and subvert their democratic will. By way of an example, we can use the idea of LGBT representation, as membership of this category would be difficult to verify for both practical and political reasons. Out of our earlier hypothetical population of 50 million, let us assume that 2% openly identify as LGBT, which would be 1 million people. This translates to 10 representatives if each represents 100,000 people.

If one homophobic person decided to claim to be LGBT for the purposes of this partitioned sortition there would be a 1 in a million chance of them being selected. Not a very big concern. What if a large number of people did this though – 100,000 homophobic people claiming to be LGBT in a coordinated attack on the democratic rights of the LGBT community?

Well, 100,000 extra people would mean that this category would gain an extra representative. 11 representatives for a category containing 1 million LGBT people and 100,000 homophobes. This works out to give a 35% probability that all 11 representatives would be LGBT =BINOM.DIST(0,11,1/11,FALSE), therefore slightly benefitting the LGBT community by overrepresenting them. There is a further 39% probability of there being exactly 1 homophobic representative =BINOM.DIST(1,11,1/11,FALSE), therefore representing this group perfectly accurately and having no effect on the LGBT community’s 10 representatives. This leaves only a 26% chance of there being more than 1 homophobe selected.

Clearly this isn’t quite as ideal as when the categories were perfectly delineated, however it is still a vast improvement on the unpartitioned sortition method. Without partitioning, the probablility of such a small group being underrepresented by at least 1 seat is 46% =BINOM.DIST(9,500,0.02,TRUE).

The worst that this situation could get is with a category that is small enough to only warrant 1 representative. If there are fewer than 100,000 people that would be members of a category, it would be inadvisable to split this category out, as although we could round up 60,000 people to having 1 representative, this could encourage a proliferation of tiny categories that would overrepresent certain groups. Further to this, allowing categories with only 60,000 people would mean that 80,000 others could fraudulently join the category, leaving it still with only 1 representative, but with the fraudulent members having a higher chance of being selected than the real members.

If we put a floor of 100,000 on the minimum category size, something similar could still happen, in which just few enough people opt into this category to avoid it gaining a second representative. This would give a situation in which only two thirds of the category were genuine members. This is an unlikely scenario, but is of sufficient concern that small categories that only receive 1 or 2 representatives should ideally be properties of people that are verifiable in some reasonably straightforward way. Categories larger than this are much less of an issue, as demonstrated above.

In the UK

So far this system has been demonstrated with hypothetical populations, but we can now look at a real country and propose a set of partitions that allow us to capture the most representative set of representatives.

The UK has a population of 66.7 million, of which about 55 million are over 16 years old. We can therefore propose a parliament of 550 representatives, each one again representing around 100,000 people. For our first partition, using the 24 “states” suggested in the United Federal Britain post, combined with 4 age bands (under-30s, 30-44, 45-59 and over-60s) and male/female, we get 192 different categories each of which receives between 2 and 4 representatives. The smallest of these categories would probably be women under-30 in “Sussex”, with a population around 150,000 whilst the largest would probably be men aged 30-44 in Scotland (around 410,000).

To this we can add more partitions:

Ethnic Heritage	Proportion of Population	Number of Representatives
African	3.0%	17
South Asian	4.9%	27
East Asian	2.0%	11
Middle Eastern	1.1%	6
Multiple	2.0%	11
European	6.7%	37
Irish	10.0%	55
British	70.3%	386

LGBT Status	Proportion of Population	Number of Representatives
LGB	6.0%	33
Gender Non-Binary	0.4%	2
Non-LGBT	93.6%	515

Education Status	Proportion of Population	Number of Representatives
No Degree	73.1%	402
Science Degree	7.3%	40
Humanities Degree	17.9%	98
Science PhD	0.7%	4
Humanities PhD	1.0%	6

Parental Status	Proportion of Population	Number of Representatives
Non-Parents	20.0%	110
Parents of Dependent Children	18.0%	99
Parents of Adults	62.0%	341

Employment Status	Proportion of Population	Number of Representatives
Doctors	0.5%	3
Nurses	1.2%	7
Other Health	6.4%	35
Teachers	0.9%	5
Other Education	5.5%	30
Police	0.2%	1
Military	0.4%	2
Other Public Sector	3.3%	18
Accountants	0.5%	3
Lawyers	0.3%	1
Other Professional, Scientific & Technical	3.9%	22
Agriculture, forestry & fishing	0.6%	4
Mining, energy and water supply	1.0%	6
Manufacturing	5.6%	31
Construction	4.4%	24
Wholesale, retail & repair of motor vehicles	7.5%	42
Transport & Storage	3.0%	16
Accommodation & Food	3.3%	18
IT & Communications	2.5%	14
Finance, Insurance, Real estate	3.1%	17
Admin, Support & Other Services	6.4%	35
Full time education	3.4%	19
Looking for work	3.8%	21
Not in employment	32.05%	176

These 6 different partitions covering location/age/gender, ethnicity, LGBT status, education status, parental status and employment should ensure a parliament that is truly representative of the electorate. This is not exhaustive though – there is no reason more partitions could not be added, were they deemed necessary or benefical.

Individual Impact

We can calculate the chances of any particular individual being selected over the course of their life. If life expectancy is 85 years and anyone over the age of 16 can be selected, this gives people 60 years of being in the electorate. Assuming people are selected for a 6-month term, this gives them on average 120 chances of being picked.

In 120 rolls of a 100,000 sided die, the probability of getting a 1 is 0.12%, or slightly less than 1 in 800 =1-BINOM.DIST(0,120,1/100000,FALSE). This means that the likelihood of any individual being picked is still very small, but that most people will know a couple of friends of friends that get selected.

Its impact on companies can be calculated too – an employee taking a 6-month sabbatical isn’t the end of the world, but it is still a bit inconvenient. If a company has 1000 employees, the probability of having one or more of them be selected in any given year is a fairly manageable 2% =1-BINOM.DIST(0,1000*2,1/100000,FALSE).

One issue to consider when implementing this system would be people that were unwilling or unable to serve. Students with exams and entrepreneurs with fledgling businesses may wish to recuse themselves, and the selection process would need to filter for ongoing mental health issues or cognitive disorders. Neither of these should be problematic on an individual basis, as jury duty already manages these same concerns, however it could become important if a particular category of people within one of the partitions experiences any of these issues disproportionately.

If 50% of the people in a category recuse themselves from selection, this doubles the chances of the remaining people being selected, which could encourage people to fraudulently claim membership of that category. Unlike the example using LGBT categories earlier, this would increase the likelihood of these fraudulent members being selected. As such, this would need to be considered when creating any category within a partition. Any categories with too high a rate of recusal would either be best avoided, or would need some form of verification for members which would increase the administrative burden.

As mentioned above, with only 6 months to a year to familiarise themselves with the issues, formulate an informed opinion, negotiate with their colleagues and implement a legislative decision, this system would rely on civil servants to help this body of ordinary citizens to be effective, and provide a long term institutional memory. This is similar to how the UK’s Parliament currently works, so it shouldn’t be too unthinkable, but it is still a step into the unknown.

This said, sortition could not be used for the executive branch of the government. Presidents, Prime Ministers, Governors and Cabinets are roles that demand competence and experience. This system would therefore not eliminate all voting, as it would still be necessary to democratically elect anyone that would be given executive power. Voting methods for this have been discussed in a previous post.

When the two forms of election, that by vote and that by lot, are mixed, the first should be used to fill places which require men of special talents, such as military offices; the other, when good sense, justice, and integrity are sufficient, as they are in judicial offices; for in a well-constituted State these qualities are common to all the citizens.

Rousseau, On the Social Contract

Ultimately, it remains to be seen whether a system that selects representatives randomly can be at all palatable to countries that have previously voted for their representatives. At least with the approach of Partitioned Sortition, we can now guarantee proportionality in all fields that are deemed important, rather than leaving it to chance.

For more discussion of Sortition, check out the books Against Elections by David Van Reybrouck and The Principles of Representative Government by Bernard Manin. There are also several communities and organisations pursuing this policy – Democracy Without Elections, the Sortition Foundation and Equality by Lot.